House Price快速构建一个BaseLine模型

Reading time ~2 minutes

1 加载数据及探索性可视化

在构建模型之前了解并且分析数据是非常重要的，并且数据集的分析是整个建模过程中最耗时的工作。 在第一个章节中，我们详细介绍一下怎么样规范化的分析数据。

1.1 了解所有的变量

在拿到数据之后，我们首先需要获取数据的信息的所有字段并进行详细阅读，每一个字段的含义。以及对应字段和我们的 目标之间的关系。还是以House price为例。为了规范数据变量的分析，我们可以列出一个这样的表格

变量名 描述 类型 分类 期望 结论 评价
OverallQual 房屋的整体质量 categorical 强相关      
YearBuilt 房屋的建造时间 categorical 强相关      
TotalBsmtSF 房屋的总体面积 numerical 强相关      
GrLivArea 房屋的使用面积 numerical 强相关      
… … … … … … …

其中不同字段的含义如下:

  • 变量名: 包含了所有跟目标可能相关的变量名称
  • 描述: 给出了变量相关的含义
  • 类型: 给出了对应变量的类型，包括数值型(numerical)和分类类型(categorical)
  • 分类: 表示对该变量描述的类型的分类，例如: house price可以分成building(表示房子的基本状况)， space(表示房子的空间大小)， location(表示房值的地理位置) space(表示房子的空间大小)， location(表示房值的地理位置)
  • 期望: 表示根据直觉，这个变量对label(在这里是价格)的影响，可以分为三个等级:高、中、低
  • 结论: 最后得出的相关性结论。(高、中、低)
  • 评价: 可以记录所有关于这个特征的想法

在了解了所有的变量之后，我们对所有的变量有了大致的影响以及基本的期望，这个期望根据直觉得来， 在此基础上通过进一步的数据验证得到结论。

1.2 单变量分析及探索性可视化

在对变量有了大致了解之后，我们首先来分析一下价格数据。

train_data = pd.read_csv('/kaggle/input/house-prices-advanced-regression-techniques/train.csv')
train_data['SalePrice'].describe()

count      1460.000000
mean     180921.195890
std       79442.502883
min       34900.000000
25%      129975.000000
50%      163000.000000
75%      214000.000000
max      755000.000000
Name: SalePrice, dtype: float64

1.查看价格的分布

import seaborn as sns
sns.distplot(train_data['SalePrice'])
print("Skewness: %f" % train_data['SalePrice'].skew())
print("Kurtosis: %f" % train_data['SalePrice'].kurt())


Skewness: 1.882876
Kurtosis: 6.536282

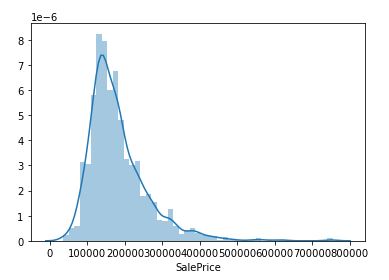
根据上面的结果可知:

  • 价格的分布偏离了正态分布
  • 计算得到偏离度为:1.882876
  • 计算得到的峰度为:6.536282

2. 分析价格和数值型变量的相关性

var = 'GrLivArea'
data = pd.concat([train_data['SalePrice'], train_data[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));
var = 'TotalBsmtSF'
data = pd.concat([train_data['SalePrice'], train_data[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));

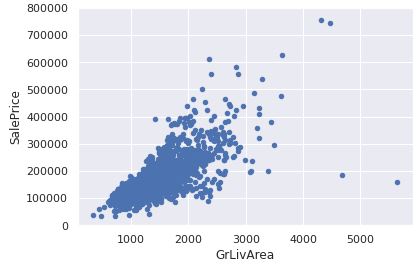
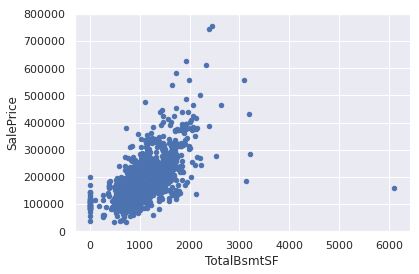
3. 分析价格和离散变量的相关性

  • 房屋整体质量和价格的关系 
    var = 'OverallQual'
data = pd.concat([train_data['SalePrice'], train_data[var]], axis=1)
f, ax = plt.subplots(figsize=(8, 6))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);
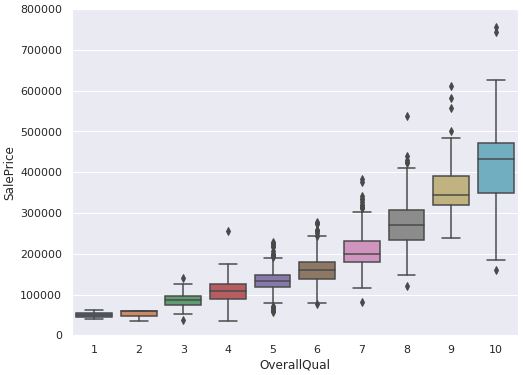
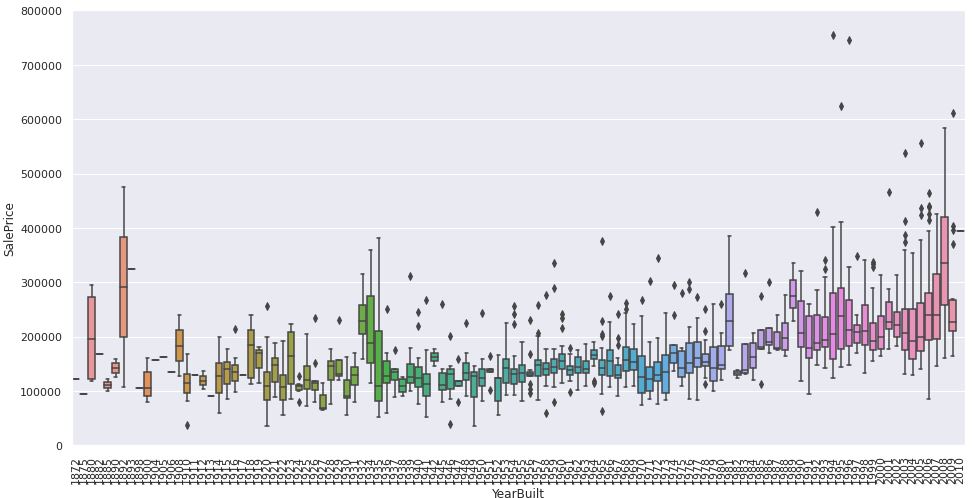
  • 房屋建造时间和价格的关系
var = 'YearBuilt'
data = pd.concat([train_data['SalePrice'], train_data[var]], axis=1)
f, ax = plt.subplots(figsize=(16, 8))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);
plt.xticks(rotation=90);

1.3. 重要变量的相关性分析

1.3.1 变量之间的相关性分析

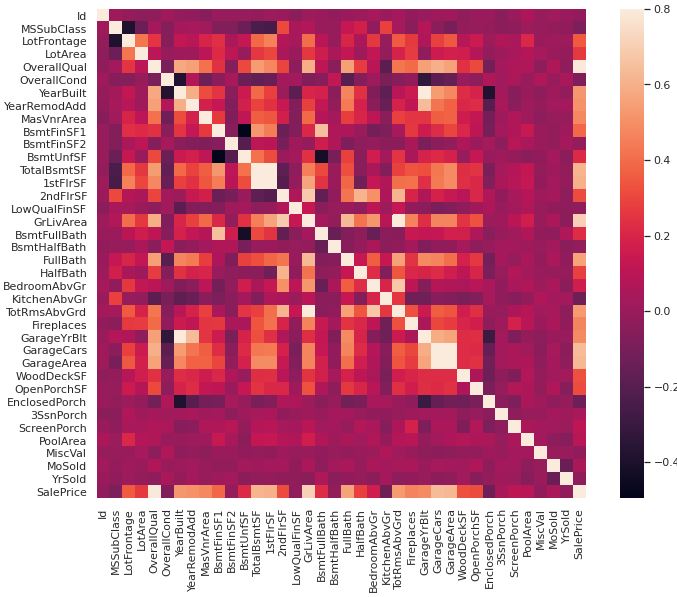
在上面我们挑选出的四个特征(2个离散特征，2个连续特征)作了一些探索性的可视化， 那么为了更好的处理全量数据，我们通过绘制热力图来分析分析变量之间的关系，以及所有变量 和SalePrice之间的关系。

corrmat = train_data.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True);

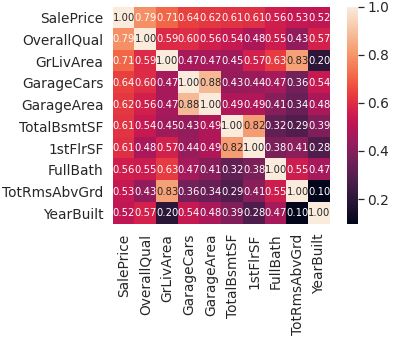
在此基础上挑选出和价格最为相关的10个变量计算热力图。

k = 10 #number of variables for heatmap
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(train_data[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, \
fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()

1.3.2 多变量分析

在上述单变量相关性处理的基础上，我们分析了不同变量和SalePrice之间的相关性系数。在此基础上我们进一步分析 这几个变量之间的关系。

#scatterplot
sns.set()
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF', 'FullBath', 'YearBuilt']
sns.pairplot(train_data[cols], size = 2.5)
plt.show();

根据整个矩阵图可以看出，我们可以看出数据集中两两变量之间的相关性。根据图结果，也可以得到和热力图类似的结论。 在相关性分析中。我们发现OverallQual是所有变量中与SalePrice最相关的变量。

2. 数据清洗

在对数据有了一个大体的了解之后，需要进一步的清洗数据，数据的清洗步骤主要包括以下两个步骤

  • 缺失值处理
  • 类别变量的处理

2.1 缺失值处理

不管是在实际的生产当中，还是在比赛数据集当中，对缺失值的处理是整个数据清洗当中 不可缺少的一部分。在这一个小节中主要介绍一下如何处理缺失数据。

在处理缺失数据的时候，我们需要考虑这样两个问题:

  1. 缺失数据量有多大

  2. 缺失的数据是随机的还是具有一定的模式。

实际处理问题过程中，这两个问题的答案对于我们来说非常重要。如果存在大量的数据缺失，我们没有办法进一步的分析 数据情况。另外一方面，我们希望缺失数据的处理过程不存在偏差。

2.1.1 统计缺失值的占比

我们对所有的变量统计一下缺失值的量以及缺失值的占比，具体的代码如下:

total = train_data.isnull().sum().sort_values(ascending=False)
percent = (train_data.isnull().sum()/
        .isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(20)

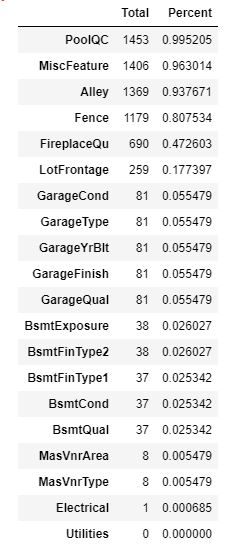
通过上面的表格我们可以得到训练数据中变量的缺失数目，以及缺失值的占比，接下来我们分别来看一下这些变量。 在这里我主要挑选三组变量来做一下缺失值的插入，其他缺失值也根据类似的方法进行处理。

1. Pool 相关变量

PoolQC和Pool Area是跟泳池有关的变量，其中PoolQuality是泳池的质量，PoolArea表示泳池的面积。 根据关于变量PoolQC的描述如下:

PoolQC: Pool quality

  • Ex        Excellent
  • Gd        Good
  • TA        Average/Typical
  • Fa        Fair
  • NA        No Pool

根据数据描述可知，NA在PoolQC这个变量里面是有意义的，当PoolAre=0的时候表示这个房子没有泳池。这个时候我们可以将PoolQC不同的value对应不同的值具体如下: PoolQC: Pool quality

  • Ex        Excellent        0
  • Gd        Good        1
  • TA        Average/Typical        2
  • Fa        Fair        3
  • NA        No Pool        4

2. Garage相关变量

在所有的变量数据中和Garage相关的变量主要有7个(GarageType, GarageYrBlt, GarageFinish, GarageCars, GarageArea, GarageQual, GarageCond)

不同变量对应的缺失频次如下:

变量名 缺失频次
GarageType 81
GarageYrBlt 81
GarageFinish 81
GarageCars 0
GarageArea 0
GarageQual 81
GarageCond 81

GarageCars和GarageArea

  • GarageCars: 表示停放车辆的数目
  • GarageArea: 表示车库的面积

GarageYrBlt

在处理GarageYrBlt变量的时候，直接通过YearBuilt变量对应的值进行填充。

GarageType， GarageFinish， GarageQual和GarageCond

在训练数据中，关于GarageType,GarageFinish,GarageQual和GarageCond变量可以分为两种情况处理。

  • 有Garage的情况: 用特定字段表示Garage缺失。
  • 没有Garage的情况: 针对数据类型，填充数据。

在训练的数据中所有缺失值都是没有Garage的，那么可以添加一个字段NA表示没有Garage的情况。

3. Electrical变量

首先查看一下Electrical变量的相关描述和数据缺失情况。

Electrical变量对应的相关描述如下:

Electrical: Electrical system

  • SBrkr        Standard Circuit Breakers & Romex
  • FuseA        Fuse Box over 60 AMP and all Romex wiring (Average)
  • FuseF        60 AMP Fuse Box and mostly Romex wiring (Fair)
  • FuseP        60 AMP Fuse Box and mostly knob & tube wiring (poor)
  • Mix        Mixed

对应不同value在训练数据集中出现的频次：

SBrkr FuseA FuseF FuseP Mix
1334 94 27 3 1

Electrical 变量只有一个缺失值并且是category类型的变量。这里我们直接选取所有category中出现频次最高的变量 作为缺失值的填充。

train_data['Electrical'][train_data['Electrical'].isnull()] = train_data['Electrical'].value_counts().keys()[0]
train_data['Electrical'].value_counts()

填充后的数据如下:

SBrkr FuseA FuseF FuseP Mix
1335 94 27 3 1

2.2 变量的转化

2.2.1 统计学中的变量分类

在统计学中，将变量的类型分为以下几种:

  • 定类变量: 定类变量表示名义级数据，是最低级的数据类型。也就是我们所说的类别。例如男、女。
  • 定序变量: 定序变量表示个体在某个有序的变量体系中存在的位置，定序变量没法做四则运算。比如受教育程度(小学、初中、高中…)。
  • 定距变量: 定距变量表示具有间距特征的变量,有单位,但是没有绝对零点。比如温度和年份等。
  • 定比变量: 最高等级的数据，既有测量单位，有绝对零点。如身高。

上述四种变量中，定类变量和定序变量统称为因子变量。

2.2.2 Label Encoding——因子变量的重编码

根据章节2.1中的操作，我们去除了数据集中所有的缺失值。目前整个数据表中包含的数据包括:因子变量和数值变量。 接下来我们看一下如何处理因子类型的变量对因子类型变量进行重编码。

在House price数据集中因子变量主要有以下几个:

  • Street: Type of road access to property
  • LandContour: Flatness of the property
  • LandSlope: Slope of property
  • Neighborhood: Physical locations within Ames city limits
  • Condition1: Proximity to various conditions
  • Condition2: Proximity to various conditions (if more than one is present)
  • BldgType: Type of dwelling
  • HouseStyle: Style of dwelling
  • RoofStyle: Type of roof
  • RoofMatl: Roof material
  • Foundation: Type of foundation
  • Heating: Type of heating
  • HeatingQC: Heating quality and condition
  • CentralAir: Central air conditioning
  • PavedDrive: Paved driveway

我们以LandSlope为例，对变量做Label Encoding。

from sklearn.preprocessing import LabelEncoder
labelencoder = LabelEncoder()
train_data["LandSlope"] = labelencoder.fit_transform(train_data["LandSlope"])
train_data["LandSlope"].value_counts()

在Label Encoding之后对每一个category变量的值有一个对应的数值类型表示。

2.2.3 将数值变量处理成因子类型

根据章节2.2.1中的介绍，我们不仅需要对字符串类型中的定类类型进行因子化重编码。 对于数值类型中的定序类型也要进行因子化重编码的操作。

1. YrSold和MoSold变量

2. MSSubClass变量

2 变量研究

3 数据清洗

4 构建baseline模型

参考资料

[1] Top 32% - House Prices Model

[2] Comprehensive data exploration with Python

[3] 左手用R右手Python系列——因子变量与分类重编码

[4] House prices: Lasso, XGBoost, and a detailed EDA

Read More

腾讯广告MVKE实现多目标的用户画像建模

以House Price为例快速构建一个Base Line模型 Continue reading

召回部分代码重构

Published on September 29, 2022

Mind多兴趣召回

Published on September 26, 2022