到底什么是NCE？

从KL散度到交叉熵

Loss 函数的目的:

假设真实分布为P, 模型训练的到的分布是Q, 训练的目的就是为了是Q分布更接近P分布。

为了计算P分布和Q分布的距离，有什么办法呢？

对于模型训练过程来说，真实分布是固定的，对于上面的公式只得到了一个:

如果需要最小化损失的话，只需要最小化上面这个公式即可。

从交叉熵和softmax结合

对于某条离散样本计算交叉熵的过程如下:

• 二分类的情况

我们用$\hat y$ 为正样本的预测概率, $y$ 为样本的真实标签值。在二分类问题中$\sum_{i=1}^2P(x)log\;Q(x)$只有两种情况。最终得到的结果:

对手训练集上的样本, 对整体的交叉熵求平均。

• 多分类的情况

多分类情况下使用softmax计算每个样本的预测概率，每个样本计算出来的概率值我们表示为$E$

公式可以描述为:

在假的类上P(x)=0最后得到的概率只是真类上的概率和，假类在softmax的分母中起作用，对上面的公式简化为:

最小化上述公式等价于最小化:

所以在这里要搞清楚一个问题, 负采样是采样一次分类里面的正例和负例, 而不是正样本和负样本。在二分类问题中，我们预测点击的概率, 但是在多分类问题中, 我们预测的是每个类别上的概率。

我们的结果是:[1, 0, 0, 0, 0, 0, 0, 0]。

每条样本下都有一个真类和假类。也就是一条样本中包含真, 也包含假;不像二分类的情况以数据行来区分正样本和负样本。这篇文章《候选采样（candidate sampling）》也是值得一看。

从多分类到NCE

在上面的代码中, 有一个很困难的问题。计算softmax的loss的时候需要计算归一化的常数 $Z = \sum_{j=1}^n E_j$。对于超分类问题来说$n$的数目非常大，这里带来的计算量是致命的。在NCE中就是将原来的多分类问题转成了二分类问题。具体NCE为什么对真实分布的模拟是有效的我们后面再说。 在nce-loss采用中使用log-uniform分布来采样噪声分布的节点结果。nce-loss采样的函数如下:

从representation到CPC

在Auto Encoder里面对于item或者词汇的embedding表示是基于label进行的。 以item2vec为例, 例如只有两个物品:

1. 物品A是美妆类型的视频, 嵌入得到了一个Embedding A1.

这个时候，在AutoEncoder的Encoder和Decoder只是拟合了一种特定的关系，这种特定的关系无法被其他模型学习到。也就是Embedding A不能代表A的特性。 或者换一种说法Embedding A即使能够代表A的特性，但是这种特性只适合在AutoEncoder的场景下使用。这种情况下的representation是not predictive的。

为了解决这个问题，有一种方式就是将物品A和Embedding A1以及组成一个pair对，将物品B和Embedding B1组成pair对，将物品A和Embedding B1组成pair对。再将物品B和embedding A1组成pair对， 去预测embedding和item是否匹配。

这种情况下实际上是有两个任务: 一个任务用来约束两个变量是否匹配, 一个任务用来训练模型。另外一个任务用来约束输入和embedding的关系，确保向量是predictive的。

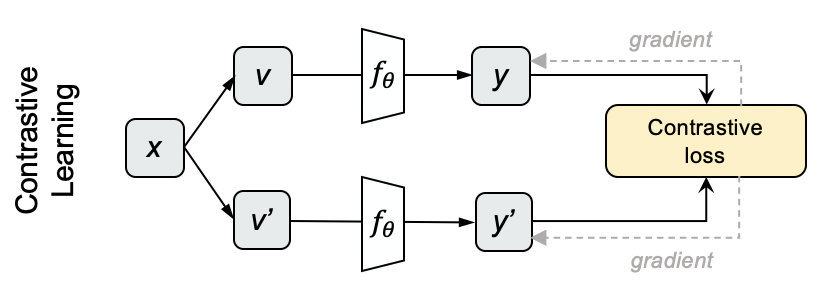
从NCE到INFO NCE

在INFO NCE中采用一个log-uniform分布来模拟噪声分布。在真实环境当中, 怎么样试图通过负样本的构建来还原真实分布是至关重要的事情。 相关INFO-NCE的代码可以参考: 腾讯iwiki

接下来到我们的重头戏: INFO-NCE 首先:INFO-NCE需要面对的问题是，高纬稀疏数据有些数据不能出现在label中的情况，这个时候没有label的那部分数据是浪费掉的。在label较少的时候怎么样把这部分数据利用起来。

这篇《理解Contrastive Predictive Coding和NCE Loss》很不。

在原始的INFO-NCE论文中, 考虑到INFO-NCE主要是用在Auto Encoder的情况。在了是的表征能力更强，我们引入一个predictive任务来预测当前的representation对物品的表示。

对于输入item A我们引入一个任务来学习item A的Embedding接下来序列的预测任务并且计算loss。一个单纯就是用来学习representation的任务和一个可以用来做预测的任务。 在NCE中，从分类转成二分类用来表示representation的结果。这种情况下是不native的。

在NCE中，将负样本的分布服从Zipfian分布。

从INFO NCE到Fcoal Loss

在目标检测当中,什么是two-stage detector和one-stage detector.

flocal loss这个函数可以减少易分类样本的权重，使得模型在训练时更专注于难分类的样本。 关注Focal loss对Loss的修改, 我们可以看一下

[1] When to Run Bandit Tests Instead of A/B/n Tests

[2] Bandit theory, part I

[3] Bandit theory, part II

[4] bgalbraith/bandits

模型的构建

在构建模型之前，为了避免从0~1先在github找一个RNN的实现，具体可以看一下参考资料[1]中实现的垃圾邮件预测算法。 在垃圾邮件预测算法中，实现了一个简单的RNN模型，我们之后在这个模型的基础上做进一步的改进。

垃圾邮件预测算法

数据集

在处理正式了解代码之前，我们先来看一下数据情况。在垃圾邮件预测算法中使用的是UCI的SMS Spam Collection Dataset 数据集。这个数据集也能在Kaggle上找到，数据链接在参考资料中给出。

SMS垃圾邮件数据集是一个SMS垃圾邮件研究标注的SMS邮件集合。在这个数据集中一共包含了5574条垃圾邮件，这些垃圾邮件 被分为两种类型:ham(legitimate)和spam。

ham Go until jurong point, crazy.. Available only in bugis n great world la e buffet… Cine there got amore wat…

ham Ok lar… Joking wif u oni…

spam Free entry in 2 a wkly comp to win FA Cup final tkts 21st May 2005. Text FA to 87121 to receive entry question(std txt rate)T&C’s apply 08452810075over18’s

ham U dun say so early hor… U c already then say…

ham Nah I don’t think he goes to usf, he lives around here though

在数据集文件中，每一行包含一条邮件信息。每一行由两列组成，第一列包含邮件的标签，第二列包含邮件的原始文本信息。

数据处理

1. 数据加载和清洗

在数据的加载和清洗阶段，主要包含以下三个部分:

• 加载数据
• 将数据切分成label和message两部分
• 去除掉message中的异常字符

text_data = []
with open(os.path.join(data_dir, data_file), 'r') as file_conn:
	for row in file_conn:
		text_data.append(row)
text_data = text_data[:-1]

text_data = [x.split('\t') for x in text_data if len(x) >= 1]
[text_data_target, text_data_train] = [list(x) for x in zip(*text_data)]

# Create a text cleaning function
def clean_text(text_string):
    text_string = re.sub(r'([^\s\w]|_|[0-9])+', '', text_string)
    text_string = " ".join(text_string.split())
    text_string = text_string.lower()
    return text_string

# Clean texts
text_data_train = [clean_text(x) for x in text_data_train]

2. 拆分训练集和测试集

在加载完成数据并去除特殊字符后，将文本数据处理成向量并且将转成正负样本。最后将得到的数据按照8:2拆分成训练 集和测试集。

# Change texts into numeric vectors
vocab_processor = tf.contrib.learn.preprocessing.VocabularyProcessor(max_sequence_length,
                                                                     min_frequency=min_word_frequency)
text_processed = np.array(list(vocab_processor.fit_transform(text_data_train)))

# Shuffle and split data
text_processed = np.array(text_processed)
text_data_target = np.array([1 if x == 'ham' else 0 for x in text_data_target])
shuffled_ix = np.random.permutation(np.arange(len(text_data_target)))
x_shuffled = text_processed[shuffled_ix]
y_shuffled = text_data_target[shuffled_ix]


# Split train/test set
ix_cutoff = int(len(y_shuffled)*0.80)
x_train, x_test = x_shuffled[:ix_cutoff], x_shuffled[ix_cutoff:]
y_train, y_test = y_shuffled[:ix_cutoff], y_shuffled[ix_cutoff:]
vocab_size = len(vocab_processor.vocabulary_)
print("Vocabulary Size: {:d}".format(vocab_size))
print("80-20 Train Test split: {:d} -- {:d}".format(len(y_train), len(y_test)))

模型结构

在将数据集处理成向量类型并且拆分成训练数据和测试数据之后，构建一个RNN模型，其具体结构如下。

# Create placeholders
x_data = tf.placeholder(tf.int32, [None, max_sequence_length])
y_output = tf.placeholder(tf.int32, [None])

# Create embedding
embedding_mat = tf.Variable(tf.random_uniform([vocab_size, embedding_size], -1.0, 1.0))
embedding_output = tf.nn.embedding_lookup(embedding_mat, x_data)

# Define the RNN cell
# tensorflow change >= 1.0, rnn is put into tensorflow.contrib directory. Prior version not test.
if tf.__version__[0] >= '1':
    cell = tf.contrib.rnn.BasicRNNCell(num_units=rnn_size)
else:
    cell = tf.nn.rnn_cell.BasicRNNCell(num_units=rnn_size)

output, state = tf.nn.dynamic_rnn(cell, embedding_output, dtype=tf.float32)
output = tf.nn.dropout(output, dropout_keep_prob)

# Get output of RNN sequence
output = tf.transpose(output, [1, 0, 2])
last = tf.gather(output, int(output.get_shape()[0]) - 1)

weight = tf.Variable(tf.truncated_normal([rnn_size, 2], stddev=0.1))
bias = tf.Variable(tf.constant(0.1, shape=[2]))
logits_out = tf.matmul(last, weight) + bias

# Loss function
losses = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=logits_out, labels=y_output)
loss = tf.reduce_mean(losses)

accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.argmax(logits_out, 1), tf.cast(y_output, tf.int64)), tf.float32))

optimizer = tf.train.RMSPropOptimizer(learning_rate)
train_step = optimizer.minimize(loss)

init = tf.global_variables_initializer()
sess.run(init)

在上述代码中各个变量的含义:

• embedding_mat: 输入数据(vocabulary)的embedding矩阵，
• embedding_output: 神经网络第一层(embedding 层)的数据数据，对应为多个神经元的look up操作。
• cell: 定义了一个基本的RNN实现的实例。
• output: RNN在一个输入序列上输出的结果。
• state: RNN在一个输入序列上输出的state。
• weight: softmax层的权重
• bias: softmax层的bias
• logits_out: RNN输出对每一个类的概率。
• losses: 每一条输入数据的loss值
• loss: 整个batch的平均loss值
• accuracy: RNN模型预测结果和真实label相比的准确率。
• optimizer: RNN上定义的优化器。

除了有关变量的含义之外，上述代码中需要重点注意的几个点包括以下内容:

1. RNNCell是什么?

RNNCell是一个抽象类。在RNNCell的子类中实现了一些常见的RNN结构。在代码中实例化了个BasicRNNCell。 这个BasicRNNCell实现了一个基本的RNN结构。

在模型训练的过程中，将一个embedding序列输入到RNNCell当中去，就可以完成这个Sequence的训练。

RNNCell的实现可以是基本的RNN，也可以是一个LSTM结构，当然也可以是GRU，此外我们在开发的时候可以自定义一个 符合自己需求的RNNCell实现子类。

2. dynamic_rnn是什么?

调用dynamic_rnn表示在训练过程中对一个sequence做动态展开，也就是每一个sequence 不同的time stamp之间 是通过一个while循环在时间维度上动态完成。

与dynamic_rnn相对应的是静态时间展开，也就是static_rnn。使用静态时间展开，在模型训练之前会将RNN序列 的动态结构展开成图结构。使用static_rnn的时候，需要将sequence length保持定长。

两者对比的区别如下，前者为动态展开，后者为静态展开。

3. 为什么使用sparse_softmax_cross_entropy_with_logits计算损失?

如果转成softmax_cross_entropy_with_logits出现如下错误，

tensorflow.python.framework.errors_impl.InvalidArgumentError: logits and labels must be broadcastable: logits_size=[250,2] labels_size=[1,250]

在使用softmax_cross_entropy_with_logits的时候计算出来的logit和label的维度不对等。因为在label中没有转成one hot的方式。

4. 为什么使用RMSPropOptimizer作为优化器?

因为RMSPropOptimizer对RNN效果很好。

模型训练

在模型训练的过程中对每一个epoch，首先对训练数据做一下shuffle。在对数据完成shuffle的基础上，分batch进行训练。 在训练阶段dropout的概率为0.5，测试阶段dropout的概率为1.0。

for epoch in range(epochs):

    # Shuffle training data
    shuffled_ix = np.random.permutation(np.arange(len(x_train)))
    x_train = x_train[shuffled_ix]
    y_train = y_train[shuffled_ix]
    num_batches = int(len(x_train)/batch_size) + 1
    # TO DO CALCULATE GENERATIONS ExACTLY
    for i in range(num_batches):
        # Select train data
        min_ix = i * batch_size
        max_ix = np.min([len(x_train), ((i+1) * batch_size)])
        x_train_batch = x_train[min_ix:max_ix]
        y_train_batch = y_train[min_ix:max_ix]

        # Run train step
        train_dict = {x_data: x_train_batch, y_output: y_train_batch, dropout_keep_prob:0.5}
        sess.run(train_step, feed_dict=train_dict)

    # Run loss and accuracy for training
    temp_train_loss, temp_train_acc = sess.run([loss, accuracy], feed_dict=train_dict)
    train_loss.append(temp_train_loss)
    train_accuracy.append(temp_train_acc)

    # Run Eval Step
    test_dict = {x_data: x_test, y_output: y_test, dropout_keep_prob:1.0}
    temp_test_loss, temp_test_acc = sess.run([loss, accuracy], feed_dict=test_dict)
    test_loss.append(temp_test_loss)
    test_accuracy.append(temp_test_acc)
    print('Epoch: {}, Test Loss: {:.2}, Test Acc: {:.2}'.format(epoch+1, temp_test_loss, temp_test_acc))

推荐数据集上构建RNN模型

基于YouTube DNN对多分类问题处理的思想，这里我们套用RNN的模型结构，将原来垃圾邮件分类中的二分类问题，处理成为 一个多分类问题。由于分类数过多，为了避免softmax层过多的数据计算，这里我们依旧采用sampling-base approach方法 对负样本数据进行采样。

构建BaseLine模型

在最基本的模型结构中，不引入其他特征，只采用用户行为序列原始数据作为输入序列。

构建离线评估指标

加入其他特征

[1] Implementing RNN for Spam Prediction

[2] SMS Spam Collection Dataset

[3] 优化方法与TensorFlow程序用例

特征工程中的缺失值补插

因为各种各样的原因，在现实世界中的数据包含各种各样的缺失值，通常以空白、NaN或者其他占位符表示。这样的数据 和scikit-learn的不相兼容，在scikit-learn中假设所有的数据是数值型的数组，并且这些数据都是有具体意义的。在处理 这些不兼容数据的时候，一个最基本的策略就是丢弃对应的行或者对应的列。这种策略的代价是丢失可能丢失掉有价值的数据。 一个更好的策略就是对这些数据进行imputation(补插)以填充数据缺失字段。

1. Univariate vs. Multivariate Imputation

在变量的补插当中，一种最基本的补插方法是单变量补插(Univariate Imputation)。补插第i个特征的数据的时候，我们只需要 使用在这个特征中所有没有缺失的数据进行插入。

多变量补插(Multivariate Imputation)和单变量的补插相对，多变量补插算法使用整个数据的变量特征来估计缺失数据。

2. Univariate Imputation

在scikit-learn的SimpleImputer类中提供了最基本的缺失值补插策略。缺失值可以插入一个提供的常量，或者使用这个特征 所在列的均值、中间值或者最高频率的值。这个类也同样支持对不同的缺失值进行编码。

在接下来的例子中给出了怎么样使用均值来补插特征中的包含的np.nan数据缺失。

>>> import numpy as np
>>> from sklearn.impute import SimpleImputer
>>> imp = SimpleImputer(missing_values=np.nan, strategy='mean')
>>> imp.fit([[1, 2], [np.nan, 3], [7, 6]])
SimpleImputer()
>>> X = [[np.nan, 2], [6, np.nan], [7, 6]]
>>> print(imp.transform(X))
[[4.          2.        ]
 [6.          3.666...]
 [7.          6.        ]]

当然这个SimpleImputer也支持Sparse矩阵

>>> import scipy.sparse as sp
>>> X = sp.csc_matrix([[1, 2], [0, -1], [8, 4]])
>>> imp = SimpleImputer(missing_values=-1, strategy='mean')
>>> imp.fit(X)
SimpleImputer(missing_values=-1)
>>> X_test = sp.csc_matrix([[-1, 2], [6, -1], [7, 6]])
>>> print(imp.transform(X_test).toarray())
[[3. 2.]
 [6. 3.]
 [7. 6.]]

当然SimplerImputer也支持用字符串或者pandas类别表示的定类数据。在填充定类的数据的时候包含most_frequent策略 和constant策略。其中most_frequent表示用高频类别填充，constant表示用固定类别填充。

>>> import pandas as pd
>>> df = pd.DataFrame([["a", "x"],
...                    [np.nan, "y"],
...                    ["a", np.nan],
...                    ["b", "y"]], dtype="category")
...
>>> imp = SimpleImputer(strategy="most_frequent")
>>> print(imp.fit_transform(df))
[['a' 'x']
 ['a' 'y']
 ['a' 'y']
 ['b' 'y']]

3. Multivariate feature imputation

当然，还有更为复杂的imputation方式。在数据处理的时候可以使用scikit-learn中的IterativeImputer类。 在这个类中，对每一个包含缺失值的数据特征，采用其他特征进行建模并对相应的缺失值进行预估。这个类以循环迭代 的方式进行:在每一次迭代中，处理一个缺失的特征列y，并且将其他特征作为输入X。然后在(X,y)上训练一个回归器 这样就可以通过预测得到y的值。在每一轮迭代中，分别对每个缺失值进行预测，并最终返回补插完后的结果。

>>> import numpy as np
>>> from sklearn.experimental import enable_iterative_imputer
>>> from sklearn.impute import IterativeImputer
>>> imp = IterativeImputer(max_iter=10, random_state=0)
>>> imp.fit([[1, 2], [3, 6], [4, 8], [np.nan, 3], [7, np.nan]])
IterativeImputer(random_state=0)
>>> X_test = [[np.nan, 2], [6, np.nan], [np.nan, 6]]
>>> # the model learns that the second feature is double the first
>>> print(np.round(imp.transform(X_test)))
[[ 1.  2.]
 [ 6. 12.]
 [ 3.  6.]]

3.1 迭代器的灵活性

在R中有许多构建好的imputation包例如:Amelia, mi, mice, missForest等等。其中missForest是最重要的一个库， 这个库是不同的imputation库的一个重要实现。这些算法都能够通过把回归器传入到IterativeImputer中来预测 缺失的特征值。在missForest中，这个回归器是随机森林。

3.2

4 Nearest neighbors imputation

在KNNImputer类中提供了一个方法用K近邻来填充缺失值。在默认情况下，KNNImputer支持欧氏距离来寻找最近邻。 每个确实值的imputation值是其最近的K个邻居在这个特征上对应的值。我们将这些邻居的在这个特征上的取值求平均 或者通过距离进行加权。如果一条数据有多个缺失值，对于不同特征上的进行的imputation可以有不同的邻居节点。 如果整个数据集上不够k个邻居或者是没有定义距离的度量， 那么这个时候选取数据集上这个特征字段的平均值作为imputation值。

关于KNNImputer的使用Demo如下:

>>> import numpy as np
>>> from sklearn.impute import KNNImputer
>>> nan = np.nan
>>> X = [[1, 2, nan], [3, 4, 3], [nan, 6, 5], [8, 8, 7]]
>>> imputer = KNNImputer(n_neighbors=2, weights="uniform")
>>> imputer.fit_transform(X)
array([[1. , 2. , 4. ],
       [3. , 4. , 3. ],
       [5.5, 6. , 5. ],
       [8. , 8. , 7. ]])

5 Marking imputed values

在scikit-learn中MissingIndicator可以将数据集中的数据转换为一个二进制矩阵从而指示缺失值的存在。在中转化 和imputation一起使用是非常有效的。在做缺失数据的imputation的时候， 保存哪些数据是丢失的可以提供一些额外的信息。

值得注意的是在SimplerImputer和IterativeImputer中存在一个bool类型的参数用来指示是否需要添加MissingIndicator.

在下面的例子中给出了MissingIndicator使用的例子，其中我们用-1表示缺失值:

>>> from sklearn.impute import MissingIndicator
>>> X = np.array([[-1, -1, 1, 3],
...               [4, -1, 0, -1],
...               [8, -1, 1, 0]])
>>> indicator = MissingIndicator(missing_values=-1)
>>> mask_missing_values_only = indicator.fit_transform(X)
>>> mask_missing_values_only
array([[ True,  True, False],
       [False,  True,  True],
       [False,  True, False]])

[1] Imputation of missing values

1 加载数据及探索性可视化

在构建模型之前了解并且分析数据是非常重要的，并且数据集的分析是整个建模过程中最耗时的工作。 在第一个章节中，我们详细介绍一下怎么样规范化的分析数据。

1.1 了解所有的变量

在拿到数据之后，我们首先需要获取数据的信息的所有字段并进行详细阅读，每一个字段的含义。以及对应字段和我们的 目标之间的关系。还是以House price为例。为了规范数据变量的分析，我们可以列出一个这样的表格

其中不同字段的含义如下:

• 变量名: 包含了所有跟目标可能相关的变量名称
• 描述: 给出了变量相关的含义
• 类型: 给出了对应变量的类型，包括数值型(numerical)和分类类型(categorical)
• 分类: 表示对该变量描述的类型的分类，例如: house price可以分成building(表示房子的基本状况)， space(表示房子的空间大小)， location(表示房值的地理位置) space(表示房子的空间大小)， location(表示房值的地理位置)
• 期望: 表示根据直觉，这个变量对label(在这里是价格)的影响，可以分为三个等级:高、中、低
• 结论: 最后得出的相关性结论。(高、中、低)
• 评价: 可以记录所有关于这个特征的想法

在了解了所有的变量之后，我们对所有的变量有了大致的影响以及基本的期望，这个期望根据直觉得来， 在此基础上通过进一步的数据验证得到结论。

1.2 单变量分析及探索性可视化

在对变量有了大致了解之后，我们首先来分析一下价格数据。

train_data = pd.read_csv('/kaggle/input/house-prices-advanced-regression-techniques/train.csv')
train_data['SalePrice'].describe()

count      1460.000000
mean     180921.195890
std       79442.502883
min       34900.000000
25%      129975.000000
50%      163000.000000
75%      214000.000000
max      755000.000000
Name: SalePrice, dtype: float64

1.查看价格的分布

import seaborn as sns
sns.distplot(train_data['SalePrice'])
print("Skewness: %f" % train_data['SalePrice'].skew())
print("Kurtosis: %f" % train_data['SalePrice'].kurt())


Skewness: 1.882876
Kurtosis: 6.536282

根据上面的结果可知:

• 价格的分布偏离了正态分布
• 计算得到偏离度为:1.882876
• 计算得到的峰度为:6.536282

2. 分析价格和数值型变量的相关性

var = 'GrLivArea'
data = pd.concat([train_data['SalePrice'], train_data[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));
var = 'TotalBsmtSF'
data = pd.concat([train_data['SalePrice'], train_data[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));

3. 分析价格和离散变量的相关性

• 房屋整体质量和价格的关系

  var = 'OverallQual'
  data = pd.concat([train_data['SalePrice'], train_data[var]], axis=1)
  f, ax = plt.subplots(figsize=(8, 6))
  fig = sns.boxplot(x=var, y="SalePrice", data=data)
  fig.axis(ymin=0, ymax=800000);
  

• 房屋建造时间和价格的关系

var = 'YearBuilt'
data = pd.concat([train_data['SalePrice'], train_data[var]], axis=1)
f, ax = plt.subplots(figsize=(16, 8))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);
plt.xticks(rotation=90);

1.3. 重要变量的相关性分析

1.3.1 变量之间的相关性分析

在上面我们挑选出的四个特征(2个离散特征，2个连续特征)作了一些探索性的可视化， 那么为了更好的处理全量数据，我们通过绘制热力图来分析分析变量之间的关系，以及所有变量 和SalePrice之间的关系。

corrmat = train_data.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True);

在此基础上挑选出和价格最为相关的10个变量计算热力图。

k = 10 #number of variables for heatmap
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(train_data[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, \
fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()

1.3.2 多变量分析

在上述单变量相关性处理的基础上，我们分析了不同变量和SalePrice之间的相关性系数。在此基础上我们进一步分析 这几个变量之间的关系。

#scatterplot
sns.set()
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF', 'FullBath', 'YearBuilt']
sns.pairplot(train_data[cols], size = 2.5)
plt.show();

根据整个矩阵图可以看出，我们可以看出数据集中两两变量之间的相关性。根据图结果，也可以得到和热力图类似的结论。 在相关性分析中。我们发现OverallQual是所有变量中与SalePrice最相关的变量。

2. 数据清洗

在对数据有了一个大体的了解之后，需要进一步的清洗数据，数据的清洗步骤主要包括以下两个步骤

• 缺失值处理
• 类别变量的处理

2.1 缺失值处理

不管是在实际的生产当中，还是在比赛数据集当中，对缺失值的处理是整个数据清洗当中 不可缺少的一部分。在这一个小节中主要介绍一下如何处理缺失数据。

在处理缺失数据的时候，我们需要考虑这样两个问题:

1. 缺失数据量有多大

2. 缺失的数据是随机的还是具有一定的模式。

实际处理问题过程中，这两个问题的答案对于我们来说非常重要。如果存在大量的数据缺失，我们没有办法进一步的分析 数据情况。另外一方面，我们希望缺失数据的处理过程不存在偏差。

2.1.1 统计缺失值的占比

我们对所有的变量统计一下缺失值的量以及缺失值的占比，具体的代码如下:

total = train_data.isnull().sum().sort_values(ascending=False)
percent = (train_data.isnull().sum()/
        .isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(20)

通过上面的表格我们可以得到训练数据中变量的缺失数目，以及缺失值的占比，接下来我们分别来看一下这些变量。 在这里我主要挑选三组变量来做一下缺失值的插入，其他缺失值也根据类似的方法进行处理。

1. Pool 相关变量

PoolQC和Pool Area是跟泳池有关的变量，其中PoolQuality是泳池的质量，PoolArea表示泳池的面积。 根据关于变量PoolQC的描述如下:

PoolQC: Pool quality

• Ex        Excellent
• Gd        Good
• TA        Average/Typical
• Fa        Fair
• NA        No Pool

根据数据描述可知，NA在PoolQC这个变量里面是有意义的，当PoolAre=0的时候表示这个房子没有泳池。这个时候我们可以将PoolQC不同的value对应不同的值具体如下: PoolQC: Pool quality

• Ex        Excellent        0
• Gd        Good        1
• TA        Average/Typical        2
• Fa        Fair        3
• NA        No Pool        4

2. Garage相关变量

在所有的变量数据中和Garage相关的变量主要有7个(GarageType, GarageYrBlt, GarageFinish, GarageCars, GarageArea, GarageQual, GarageCond)

不同变量对应的缺失频次如下:

GarageCars和GarageArea

• GarageCars: 表示停放车辆的数目
• GarageArea: 表示车库的面积

GarageYrBlt

在处理GarageYrBlt变量的时候，直接通过YearBuilt变量对应的值进行填充。

GarageType， GarageFinish， GarageQual和GarageCond

在训练数据中，关于GarageType,GarageFinish,GarageQual和GarageCond变量可以分为两种情况处理。

• 有Garage的情况: 用特定字段表示Garage缺失。
• 没有Garage的情况: 针对数据类型，填充数据。

在训练的数据中所有缺失值都是没有Garage的，那么可以添加一个字段NA表示没有Garage的情况。

3. Electrical变量

首先查看一下Electrical变量的相关描述和数据缺失情况。

Electrical变量对应的相关描述如下:

Electrical: Electrical system

• SBrkr        Standard Circuit Breakers & Romex
• FuseA        Fuse Box over 60 AMP and all Romex wiring (Average)
• FuseF        60 AMP Fuse Box and mostly Romex wiring (Fair)
• FuseP        60 AMP Fuse Box and mostly knob & tube wiring (poor)
• Mix        Mixed

对应不同value在训练数据集中出现的频次：

Electrical 变量只有一个缺失值并且是category类型的变量。这里我们直接选取所有category中出现频次最高的变量 作为缺失值的填充。

train_data['Electrical'][train_data['Electrical'].isnull()] = train_data['Electrical'].value_counts().keys()[0]
train_data['Electrical'].value_counts()

填充后的数据如下:

2.2 变量的转化

2.2.1 统计学中的变量分类

在统计学中，将变量的类型分为以下几种:

• 定类变量: 定类变量表示名义级数据，是最低级的数据类型。也就是我们所说的类别。例如男、女。
• 定序变量: 定序变量表示个体在某个有序的变量体系中存在的位置，定序变量没法做四则运算。比如受教育程度(小学、初中、高中…)。
• 定距变量: 定距变量表示具有间距特征的变量,有单位,但是没有绝对零点。比如温度和年份等。
• 定比变量: 最高等级的数据，既有测量单位，有绝对零点。如身高。

上述四种变量中，定类变量和定序变量统称为因子变量。

2.2.2 Label Encoding——因子变量的重编码

根据章节2.1中的操作，我们去除了数据集中所有的缺失值。目前整个数据表中包含的数据包括:因子变量和数值变量。 接下来我们看一下如何处理因子类型的变量对因子类型变量进行重编码。

在House price数据集中因子变量主要有以下几个:

• Street: Type of road access to property
• LandContour: Flatness of the property
• LandSlope: Slope of property
• Neighborhood: Physical locations within Ames city limits
• Condition1: Proximity to various conditions
• Condition2: Proximity to various conditions (if more than one is present)
• BldgType: Type of dwelling
• HouseStyle: Style of dwelling
• RoofStyle: Type of roof
• RoofMatl: Roof material
• Foundation: Type of foundation
• Heating: Type of heating
• HeatingQC: Heating quality and condition
• CentralAir: Central air conditioning
• PavedDrive: Paved driveway

我们以LandSlope为例，对变量做Label Encoding。

from sklearn.preprocessing import LabelEncoder
labelencoder = LabelEncoder()
train_data["LandSlope"] = labelencoder.fit_transform(train_data["LandSlope"])
train_data["LandSlope"].value_counts()

在Label Encoding之后对每一个category变量的值有一个对应的数值类型表示。

2.2.3 将数值变量处理成因子类型

根据章节2.2.1中的介绍，我们不仅需要对字符串类型中的定类类型进行因子化重编码。 对于数值类型中的定序类型也要进行因子化重编码的操作。

1. YrSold和MoSold变量

2. MSSubClass变量

2 变量研究

3 数据清洗

4 构建baseline模型

参考资料

[1] Top 32% - House Prices Model

[2] Comprehensive data exploration with Python

[3] 左手用R右手Python系列——因子变量与分类重编码

[4] House prices: Lasso, XGBoost, and a detailed EDA